🔺 Triangolo di Tartaglia (Pascal)

Numero di righe (n ≥ 0): Genera

Triangolo di Tartaglia (o di Pascal)

Il Triangolo di Tartaglia è una celebre disposizione piramidale di numeri interi, in cui ogni elemento è ottenuto sommando i due numeri immediatamente sopra di esso nella riga precedente.

• La costruzione parte dalla riga 0, che contiene un solo numero: 1.
• Ogni riga successiva aggiunge un elemento in più e si costruisce secondo una semplice regola:
  Ogni numero è la somma dei due sovrastanti.

A cosa serve?

Il triangolo ha numerose applicazioni in matematica, tra cui:

• Il calcolo dei coefficienti binomiali C(n, k), utilizzati nello sviluppo del binomio di Newton.
• La combinatoria, per contare combinazioni e probabilità.
• L’analisi di simmetrie e strutture ricorsive nei numeri.

Vuoi esplorarlo?

Inserisci un numero n per generare le prime n + 1 righe del triangolo.
Ogni riga mostra i coefficienti binomiali C(n, k) per k = 0 fino a n.

Suggerimento: passa il cursore sopra ciascun numero per visualizzare la formula binomiale da cui deriva.

Problema pratico di combinatoria

Domanda: In quanti modi diversi si possono scegliere 3 studenti da una classe di 7 per partecipare a una gara?

Soluzione con il Triangolo di Tartaglia:

Questo è un problema di combinazioni:
Dobbiamo calcolare C(7, 3), cioè il numero di modi per scegliere 3 elementi da 7, senza tener conto dell’ordine.

Nel Triangolo di Tartaglia, troviamo questo valore:

• Vai alla riga 7 (che rappresenta n = 7)

• Prendi il quarto numero da sinistra (posizione k = 3, poiché si parte da 0)

C(7, 3) = 35

✅ Quindi, ci sono 35 combinazioni possibili di 3 studenti su 7.

sviluppo binomiale

Espressione:

Utilizzando la riga 4 del triangolo (1, 4, 6, 4, 1), possiamo sviluppare:

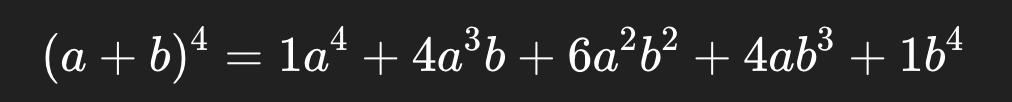
Questo sviluppo viene utilizzato in algebra, fisica (espansione di espressioni), e anche in calcolo delle probabilità (modelli binomiali).